NMR - STRUCTURAL ANALYSIS [provided by Dr. Padmanava Pradhan]
Nuclear Magnetic Resonance (NMR) is a powerful spectroscopic technique that has found applications in all spheres of scientific research. Nuclear magnetic resonance spectroscopy is used to study physical, chemical, and biological properties of matter. Like any other spectroscopic techniques NMR also involves transitions between energy levels but involves nuclear spin energy level in presence of an external magnetic field.
When the spins of the protons and neutrons in nuclei are not paired, the overall spin of the charged nucleus generates a magnetic dipole along the spin axis, and the intrinsic magnitude of this dipole is a fundamental nuclear property called the nuclear magnetic moment, μ. The symmetry of the charge distribution in the nucleus is a function of its internal structure and if this is spherical (i.e. analogous to the symmetry of a 1S hydrogen orbital), it is said to have a corresponding spin angular momentum number of I=1/2, of which examples are 1H, 13C, 15N, 19F, 31P etc. Nuclei which have a non-spherical charge distribution have higher spin numbers (eg 10B, 14N etc).
The nuclear magnetic moment of a nucleus can align with an externally applied magnetic field of strength B0 in only 2I+1 ways, either re-inforcing or opposing B0. The energetically preferred orientation has the magnetic moment aligned parallel with the applied field (spin +1/2) and is often given the notation a, whereas the higher energy anti-parallel orientation (spin -1/2) is referred to as b. In the absence of an external magnetic field, these orientations are of equal energy. If a magnetic field is applied, then the energy levels split. Each level is given a magnetic quantum number, m. The rotational axis of the spinning nucleus cannot be orientated exactly parallel (or anti-parallel) with the direction of the applied field B0 (defined in our coordinate system as about the z axis) but must precess about this field at an angle with an angular velocity given by the expression;
The constant γ is called the magnetogyric ratio and relates the magnetic moment m and the spin number I for any specific nucleus;
The frequency of precession is termed the Larmor frequency, which is identical to the transition frequency. The potential energy of the precessing nucleus is given by;
where θ is the angle between the direction of the applied field and the axis of nuclear rotation. If energy is absorbed by the nucleus, then the angle of precession, q, will change. For a nucleus of spin 1/2, absorption of radiation "flips" the magnetic moment so that it opposes the applied field (the higher energy state).
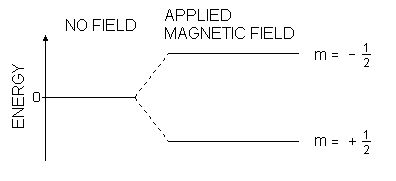
Energy levels for a nucleus with spin quantum number 1/2
Modern nmr spectrometers use powerful magnets having fields of 1 to 20 T. Even with these high fields, the energy difference between the two spin states is less than 0.1 cal/mole (infrared transitions involve 1 to 10 kcal/mole and electronic transitions are nearly 100 time greater). For nmr purposes, this small energy difference (DE) is usually given as a frequency in units of MHz (1e+06 Hz), ranging from 20 to 900 MHz, depending on the magnetic field strength and the specific nucleus being studied. Irradiation of a sample with radio frequency (rf) energy corresponding exactly to the spin state separation of a specific set of nuclei will cause excitation of those nuclei in the +1/2 state to the higher -1/2 spin state. A resonace absortion (hence a signal) occurs when the precession frequency corresponding to DE matches with the radiofrequency. In continuos wave (CW) NMR either the magnetic field or the radifrqency is varied to get resonance absorptions and the NMR signals.

A standard Varian Mercury NMR Spectrometer
FOURIER-TRANSFORM NUCLEAR MAGNETIC RESONANCE (FT-NMR) SPECTROSCOPY
Most of the modern day NMR spectrometers are Fourier-transform NMR spectrometers. FT NMR spectrometers use a pulse of radiofrequency (RF) radiation to cause nuclei in a magnetic field to flip into the higher-energy alignment. Due to the Heisenberg uncertainty principle, the frequency width of the RF pulse (typically 1-10 Ás) is wide enough to simultaneously excite nuclei in all local environments. All of the nuclei will re-emit RF radiation at their respective resonance frequencies, creating an interference pattern in the resulting RF emission versus time, known as a free-induction decay (FID). The frequencies are extracted from the FID by a Fourier transform of the time-based data. Because the FID results from the emission due to nuclei in all environments, each pulse contains an interference pattern from which the complete spectrum can be obtained. Because of this multiplex (or Fellgett) advantage, repetitive signals can be summed and averaged to greatly improve the signal-to-noise ratio of the resulting FID.
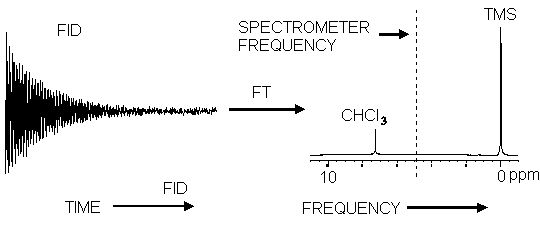
Effect of the Fourier Transform on a free induction decay
An FT-NMR spectrometer consists of a control console, magnet, and a coil of wire that serves as the antenna for transmitting and receiving the RF radiation. (Only one coil is necessary because signal reception does not begin until after the end of the excitation pulse.) Because the FID results from the emission due to nuclei in all environments, each pulse contains an interference pattern from which the complete spectrum can be obtained. Because of this multiplex (or Fellgett) advantage, repetitive signals can be summed and averaged to greatly improve the signal-to-noise ratio of the resulting FID.
CHEMICAL SHIFT
Chemical shift is the most important parameter in NMR spectroscopy arising due to the electronic environment around nuclei. The magnetic field at the nucleus is not equal to the applied magnetic field; electrons around the nucleus shield it from the applied field. The difference between the applied magnetic field and the field at the nucleus is termed the nuclear shielding. if the electrons around the nucleus are s-electrons, they produce a magnetic field that opposes the applied filed due to their spherical symmetry and circulation in the applied field. This means that the applied field strength must be increased for the nucleus to absorb at its transition frequency. This upfield shift is also termed diamagnetic shift. Electrons in p-orbitals have no spherical symmetry. They produce comparatively large magnetic fields at the nucleus, which give a low field shift. This "deshielding" is termed paramagnetic shift. In proton (1H) NMR, there are no p-orbitals.p-orbitals, which is why only a small range of chemical shift (15 ppm) is observed. We can easily see the effect of s-electrons on the chemical shift by looking at substituted methanes, CH3X. As X becomes increasingly electronegative, so the electron density around the protons decreases, and they resonate at lower field strengths (increasing dH values).
Chemical shift is a function of the nucleus and its environment. The difference of absoption frequencies between protons is very small (in Hz) compared to the applied field (MHz). Therefore, chemical shifts expressed expressed in parts per million (ppm). It is measured relative to a reference compound. For 1H NMR, the reference is usually 0 ppm for tetramethylsilane, Si (CH3)4.
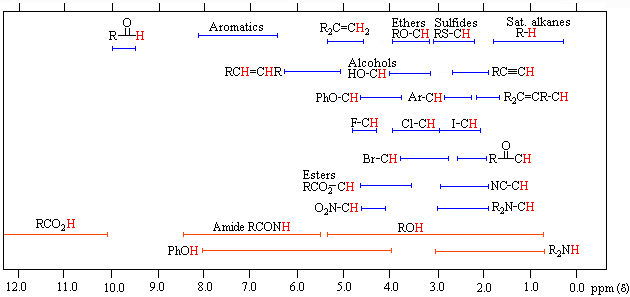
Some standard ranges of 1H NMR chemical shifts in organic compounds.
SPIN- SPIN COUPLING
Spin-spin coupling is another important parameter that arises due to a small interaction (coupling) between the nuclei (protons). For example, in the 1H NMR spectrum of ethanol (below) the methyl peak has been split into three peaks (a triplet) and the methylene peak has been split into four peaks (a quartet) due to spin-spin coupling. The spacings between the peaks of the methyl triplet are equal to the spacings between the peaks of the methylene quartet. This spacing is measured in Hertz and is called the coupling constant, J. To see why the methyl peak is split into a triplet, let's look at the methylene protons. There are two of them, and each can have one of two possible orientations (aligned with or opposed against the applied field). This gives a total of four possible states;
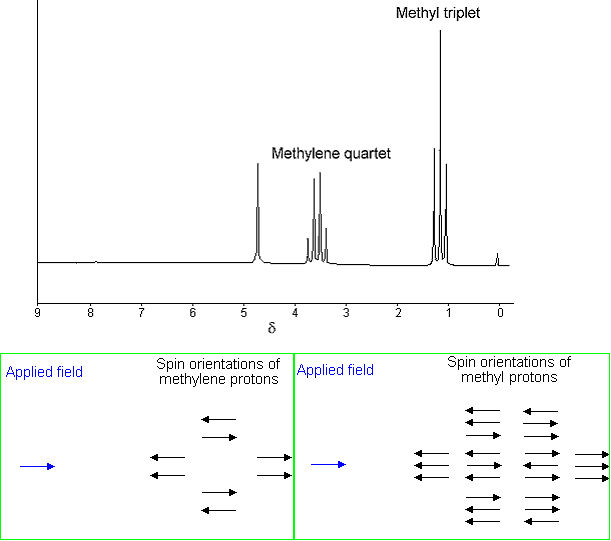
In the first possible combination, spins are paired and opposed to the field. This has the effect of reducing the field experienced by the methyl protons; therefore a slightly higher field is needed to bring them to resonance, resulting in an upfield shift. Neither combination of spins opposed to each other has an effect on the methyl peak. The spins paired in the direction of the field produce a downfield shift. Hence, the methyl peak is split into three, with the ratio of areas 1:2:1. Similarly, the effect of the methyl protons on the methylene protons is such that there are eight possible spin combinations for the three methyl protons.
Out of these eight groups, there are two groups of three magnetically equivalent combinations. The methylene peak is split into a quartet. The areas of the peaks in the quartet have the ration 1:3:3:1. In a first-order spectrum (where the chemical shift between interacting groups is much larger than their coupling constant), interpretation of splitting patterns is quite straightforward;
(1) The multiplicity of a multiplet is given by the number of equivalent protons in neighbouring atoms plus one, i.e. the n + 1 rule.
(2) Equivalent nuclei do not interact with each other. The three methyl protons in ethanol cause splitting of the neighbouring methylene protons; they do not cause splitting among themselves.
(3) The coupling constant is not dependant on the applied field. Multiplets can be easily distinguished from closely spaced chemical shift peaks.
REQUIRED MATERIALS AND APPARATUS
-NMR spectrometer (300 MHZ at J1201)
-cleaned and oven dried 5mm NMR tubes
-deuterated chloroform (CDCl3)
-two empty vials to prepare sample
-glass pipettes, rubber bulb
-samples of o- and p-toluidine: a solid (A) and a liquid (B)
-spatula
EXPERIMENTAL PROCEDURE
(1) Take out about 5mg of sample A into a clean vial using a spatula
(2) Add about 0.6 ml of CDCl3 and shake the sample to get a clear solution
(3) Transfer the sample solution in CDCl3 into a NMR tube
(4) Record 1H NMR data by locking. shimming, spinning and acquiring
(5) Save the spectrum
(6) Take out half 1/4 ml of sample B into a clean vial using a glass pipette; follow steps (2)-(5).
DATA PROCESSING
(1) Load the spectra and process it by Fourier Transformation
(2) Print out spectra with integration and peak picking as described on the procedure
(3) Tabulate the chemical shifts and coupling constants.
(4) Analysis of coupling pattern and chemical shifts will help to distinguish the isomeric toluidines (positional Isomers).


