SURFACE TENSION
Surface tension is an effect within the surface layer of a liquid that causes that layer to behave as an elastic sheet. In the bulk of the liquid each molecule is pulled equally in all directions by neighboring liquid molecules, resulting in a net force of zero. At the surface of the liquid, the molecules are pulled inwards by other molecules deeper inside the liquid but they are not attracted as intensely by the molecules in the neighbouring medium. Therefore all of the molecules at the surface are subject to an inward force of molecular attraction which can be balanced only by the resistance of the liquid to compression.
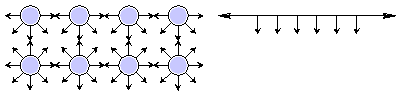
Molecules on the surface of a liquid experience an imbalance of forces
The net effect of this situation is the presence of free energy at the surface. The excess energy is called surface free energy and can be quantified as a measurement of energy per unit area. It is also possible to describe this situation as having a line tension or surface tension, which is quantified as a force per unit length measurement. The common units for surface tension are dynes/cm. Surface effects might be expressed in the language of thermodynamics,
At constant temperature and pressure the Gibbs free energy becomes,
Since γ is a positive constant under a given set of conditions we note that,
This simply means that decreasing the surface area of a substance is always spontaneous (ΔG<0), on the contrary, in order to increase its surface a certain amount of energy is needed, as the process is, per se, non-spontaneous (ΔG>0). A measure of how spontaneous (or non-spontaneous) is the change in the surface area is precisely the surface tension.
The work of surface formation at constant volume and temperature can be expressed as the change in the Helmholtz energy,
where σ is the surface area. For example:
Compute the work needed to raise a platinum-iridium alloy ring of mean circunference 5.00 cm and to stretch the surface of pure water at 20.00C through a height of 0.02 cm. The surface tension of pure water at 20.00C is 72.8 dynes/cm. Ignore gravitational effects.
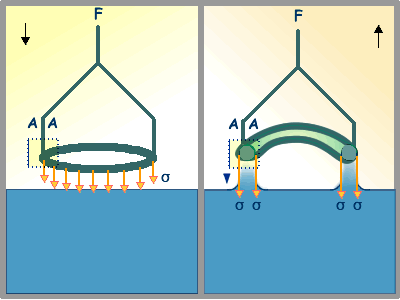
Free body diagram of the platinum-iridium alloy ring
dσ(in/out) = 0.02 cm X 5.00 cm = 0.10 cm2
dσ(both) = 2 X 0.10 cm2 = 0.20 cm2
dA = γ X dσ(both)
dA = [72.8 dynes/cm] X [0.20 cm2]
dA = 14.56 dynes X cm = 14.56 X 10-7 Joules.
Compute the weight of the heaviest platinum-iridium alloy ring of mean circunference 5.00 cm that will float in pure water at 20.00C.
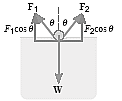
Cross section showing the forces acting on the platinum-iridium alloy ring
F1 + F2 -W = 0
(γL)cosθ + (γL)cosθ -W = 0
W = 2(γL)cosθ
W = 2(0.0728 N/m X 0.05 m)cos00 = 7.28 X 10-3 N
7.28 X 10-3 N / (9.8 m/s2) = 7.43 X 10-4 kg = 0.743 g
Du Noüy RING METHOD
Historically the Du Noüy Ring method was the first to be developed. In this class, we will be using the Surface Tensiomat Model 21 from Fisher Scientific. The modern design still contains the basic elements of a surface tensiometer that could have been built in the middle ages.

An antique tensiometer and its modern conterpart
In the Du Noüy Ring method the liquid is raised until contact with the surface is registered. The sample is then lowered again so that the liquid film produced beneath the ring is stretched. The surface tension would then be given by,
where F is the detachment force, L is the mean circunference of the ring and the factor of two (2) takes care of the inner and outher surface of the ring.
In order to understand what is going on, let's look at a graph of Force as a function of ring distance.
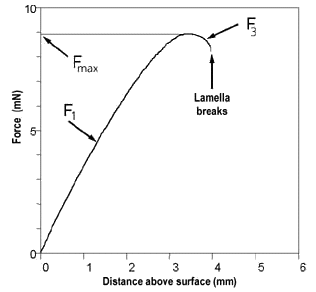
Change of force with ring distance
Suppose you are back in the old days you would have had to dip the ring just under the surface of the liquid of which you want determine the surface tension and level the balance in these conditions. At this point your graph is in the F1 range. Some masses would then be added to the opposite arm until the ring detached from the liquid. At this point your graph is either at the Fmax point or somewhere in the F3 range. Then it becomes clear that you should read the surface tension during a return movement as well and the results should agree.
But we are in the modern age now. The lowering and raising of the liquid sample is done by a motor driven mechanisn and the Suface Tensiomat Model 21 can be calibrated to read the surface tension directly in dynes/cm. Still, reproducibility of results within certain tolerance is required.
REQUIRED MATERIALS AND APPARATUS
-Surface Tensiomat Model 21
-Destilled Water
-Petri Dishes
-n-butanol (density 0.8098 g/mL)
-n-pentanol (density 0.8110 g/mL)
-thermometer
EXPERIMENTAL PROCEDURE

Main parts of the Surface Tensiomat Model 21
The operation of the Surface Tensiomat Model 21 is described in the respective Instruction Manual. For most laboratory work The following instructions should be enough.
Adjust the height of the Movable Table: It is best to obtain petri dishes that have the same diameter. That way, adding a constant volume of liquid will result in a constant liquid height and the table adjustment will need to be done only once. The liquid level in the dish should be about 1 cm. To move the table by a large distance use the table adjustment (L). To move the table by a small distance (a couple of mm) use the table adjustment (S).
Set the Zero Tension Reading: Raise the sample table until the ring is about 2 mm under the liquid. Release the tension of the machine by turning the Tension Knob. Turning the knob counterclockwise increases the tension, turning the knob clockwise decreases the tension. When the Index is aligned with its image in the mirror, the tension should be zero.
[1] Adjust the reading in the main dial to zero using the Set Zero Knob.
[2] Increase the tension until the film breaks.
[3] Release the tension, stopping at the point when the ring returns to the liquid.
[4] Readjust the reading in the main dial to zero using the Set Zero Knob.
[5] Repeat until reproducibility within a few dynes/cm is obtained.
Calibrate the Tensiometer: The readings might be a bit too small or a bit too large. However, we do not want to have to do adjust the tensiometer's mechanism thus we will have to multiply all readings by a calibration constant. For this we use distilled water at 200C, which has a surface tension of 72.8 dynes/cm.
Obtain the correction factor: Take at least five (5) measurements and assume that the mean value is a good approximation for γ. The correction factor cf for the subsequent determinations will be,
72.8 dynes/cm
--------------- = cf
γ
Every future measurement is to be multiplied by this correction factor. Notice that:
[1] If γ is smaller than 72.8 dynes/cm, then the correction factor is larger than 1.
[2] If γ is larger than 72.8 dynes/cm, then the correction factor is smaller than 1.
[3] If γ is exactly 72.8 dynes/cm, then the correction factor is exactly 1 (No correction needed).
Prepare a 0.10 M solution of n-butanol, let's call this concentration C. Dilute precisely to 1/2 of the original 0.10 M concentration, let's call this concentration C/2. Repeat as indicated in the following table,
Solution # Concentration 1 C 2 C/2 3 C/4 4 C/8 5 C/16 6 C/32Determine the surface tension and temperature of each solution. It is recommended that all measurements be made at nearly the same temperature. Take at least three readings for each concentration. Rinse and dry the ring between measurements.
Repeat the procedure with Distilled Water at the following temperatures.
Temperature 0C
1 10
2 20
3 30
4 40
5 50
6 60
DATA PROCESSING
-For the n-butanol solutions, plot the surface tension γ in the ordinate and the logarithm of the bulk concentration C in the abscissa.
-Determine the slope of the line.
-Compute the surface concentration using the Gibbs isotherm,
-Γ has units of mol per surface area in cm2. Convert cm2 to Å2, take the reciprocal of this quantity and use Avogadro's number to obtain the surface area per molecule (σ).
-The difference between the surface tension of the solvent and that of the solution, γ0-γ, is the force per centimeter exerted by the adsorbed molecules at the interface. This force per unit length is the surface pressure, π. Find π for each solution.
-Plot π as a function of σ. This is the two-dimensional isotherm analogous to the three dimensional P as a function of V graph.
-From the graph of π as a function of σ, determine the surface pressure and surface area per mole of adsorbed solute at the point of complete surface coverage (monolayer formation).
-For the distilled water trials, plot the surface tension γ in the ordinate and the temperature T in the abscissa.
-The general trend is that surface tension decreases with temperature, reaching a value of 0 at the critical temperature Tc. Extrapolate to γ = 0 and determine Tc for water.
-Use Eötvös empirical equation to estimate the molar volume of water,
-Submit all graphs with your report.
-Testing your knowledge: In the Gospel of John (John 6:16-21) Jesus is said to have walked over water. Some scholars believe this miracle involved a change in the surface tension of the water in the immediate vicinity of Jesus. Compute the surface tension of this holy region of water. According to the canonical Gospels, Jesus weighted 75 kilograms and wore sandals size 8 (USA).


